Dijkstra's Minimum Path Cost

Here we cover problems involving finding the shortest path between vertices in a graph with weights (lengths) on the edges. One obvious application is in finding the shortest route from one address to another, however shortest paths have many other application¹

Dijkstra's Algorithm

Dijkstra’s is an important algorithm both because it is an efficient algorithm for an important problem, but also because it is a very elegant example of an efficient greedy algorithm that generates optimal solutions on a nontrivial task.

The below animated image demonstrated how the algorithm works

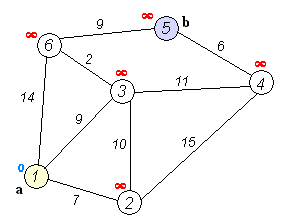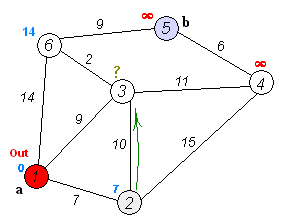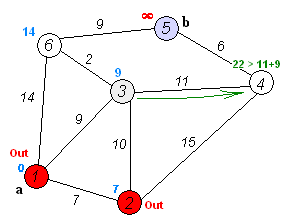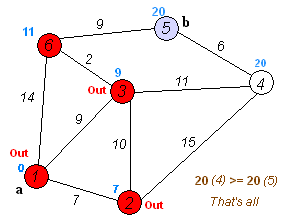
The above depiction performs the below steps

push the starting node a in the priority queue with cost 0
Pop the node with the lowest cost in the queue; at fist this is a
- if the 'node' matches our target node b
  - extract path with minimum cost
  - terminate
- For each edge node attached to the node
  - calculate cost distance
  - if edge node has cost larger to the calculated cost distance then assign cost to edge node, otherwise do not update cost
  - push (edge node, cost) to the priority queue and repeat

Prioritised Queue

Dijkstra's differentiating approach is that we must always process next the node with the lowest cost in the queue. To achieve this we have to make use of the BinaryHeap collection structure. The use of such structure help us to maintain on ordered-queue by node-cost, hence keeping the node with lowest-cost at the top of the heap/queue.

#[derive(Debug,Clone,Copy,Hash,Eq,PartialEq)]
pub enum NodeType {
    N(Node),
    NC(Node, Cost)
}
impl From<NodeType> for Node {
    fn from(nt: NodeType) -> Self {
        match nt { NodeType::N(node)|NC(node, _) => node }
    }
}
impl From<Node> for NodeType {
    fn from(value: Node) -> Self {
        NodeType::N(value)
    }
}
impl Ord for NodeType {
    fn cmp(&self, other: &Self) -> Ordering {
        other.partial_cmp(self).unwrap_or_else(|| panic!("Edge::cmp() - cannot compare nodes with type NodeType::N"))
    }
}
impl PartialOrd for NodeType {
    fn partial_cmp(&self, other: &Self) -> Option<Ordering> {
        match other {
            NodeType::N(_) => None,
            NC(_, cost) => {
                let NC(_,sc) = self else { panic!("Edge::partial_cmp() - cannot compare NodeType::NC against NodeType::N") };
                Some(cost.cmp(sc))
            }
        }
    }
}

Implementation

With the ordered-queue logic in place, we still need to have the means to maintain the following information per node and while we are searching the graph

node state, in terms of processed / not processed
parent node, that is, the node we visited from
unit in terms of cost or distance

The Tracker structure simplifies managing the node processing state of the graph, and we will use as part of our implementation.

Both Tracker and BinaryHeap structures are part the Graph processing State structure PSState which in turn, implements the BFSearch abstraction

As a result, the algorithm can now be realised by the following implementation

    fn path_shortest(&self, start: Node, goal: Node) -> Option<(Vec<Node>, Cost)> {
        /// Structure for maintaining processing state while processing the graph
        struct PSState {
            tracker: Tracker,
            queue: BinaryHeap<NodeType>
        }

        /// State Constructor from a given Graph and related shortest path initiation requirements
        impl PSState {
            fn new(g:&Graph) -> PSState {
                PSState {
                    // reset all node costs to MAX value with no path-parent nodes
                    tracker: g.get_tracker(Undiscovered, Cost::MAX, None),
                    // We are using a BinaryHeap queue in order to always have first in the queue
                    // the node with lowest cost to explore next
                    queue: BinaryHeap::new()
                }
            }
        }

        /// Implementation of Path Search abstraction
        impl BFSearch for PSState {
            type Output = (Vec<Node>,Cost);
            type QueueItem = NodeType;

            /// Processing of starting node
            fn initiate(&mut self, start: Node) -> &mut Self {
                // set cost at start node to zero with no parent node
                self.tracker[start].distance(0);
                // push start node in the BinaryHeap queue
                self.queue.push(NC(start,0));
                self
            }

            /// get the element with the lowest cost from the queue
            fn pop(&mut self) -> Option<Self::QueueItem> { self.queue.pop() }

            /// extract node from the queued item retrieved
            fn node_from_queued(&self, qt: &Self::QueueItem) -> Node {
                (*qt).into()
            }

            /// Process current node after all edges have been discovered and marked for processing
            fn post_process_node(&mut self, node: Node) {
                self.tracker[node].visited(Discovered);
            }

            /// has the given node been seen before ?
            fn is_discovered(&self, node: NodeType) -> bool { self.tracker[node.into()].is_discovered() }

            /// Process given edge and return `true` to proceed or `false` to abandon further edge processing
            fn pre_process_edge(&mut self, src:Node, dst: NodeType) -> bool {
                if let NC(dst, cost) = dst {
                    // calc the new path cost to edge
                    let edge_cost = self.tracker[src].dist + cost;
                    // if new cost is better than previously found
                    if edge_cost > self.tracker[dst].dist  {
                        // Do no process this edge any further
                        false
                    }
                    else {
                        // set the new lower cost @node along with related parent Node
                        self.tracker[dst].distance(edge_cost).parent(src);
                        // and ensure the edge is processed further
                        true
                    }
                }
                else {
                    // somehow we got the wrong NodeType here
                    panic!("pre_process_edge(): Must use NodeType::NC")
                }
            }

            /// Construct the item to be queued, that is, (Node,Cost)
            fn node_to_queued(&self, node: Node) -> Self::QueueItem {
                NC(node, self.tracker[node].dist )
            }

            /// Push into (Node,Cost) into the queue
            fn push(&mut self, item: Self::QueueItem) { self.queue.push(item) }

            /// Get search path discovered so far
            fn extract_path(&self, start: Node) -> Self::Output { self.tracker.extract(start) }
        }

        // Construct the state structure and search for a path that exists between start -> goal
        PSState::new(self).path_search(self,start,goal)

    }

References:

Shortest Path

Rusting along

Dijkstra's Minimum Path Cost

Dijkstra's Algorithm

Prioritised Queue

Implementation

References: