Shortest Distance Path

In this case, we want to determine if one vertex is reachable from another. Recall that a vertex u is reachable from v if there is a (directed) path from v to u.¹

Search Strategy: Breadth First Search (BFS) Algorithm

The breadth-first algorithm is a particular graph-search algorithm that can be applied to solve a variety of problems such as

• finding all the vertices reachable from a given vertex,
• finding if an undirected graph is connected,
• finding (in an unweighted graph) the shortest path from a given vertex to all other vertices,
• determining if a graph is bipartite,
• bounding the diameter of an undirected graph,
• partitioning graphs,
• and as a subroutine for finding the maximum flow in a flow network (using Ford-Fulkerson’s algorithm).

As with the other graph searches, BFS can be applied to both directed and undirected graphs.

BFS Approach

The idea of breadth first search is to start at a source vertex s and explore the graph outward in all directions level by level, first visiting all vertices that are the (out-)neighbors of s (i.e. have distance 1 from s), then vertices that have distance two from s, then distance three, etc. More precisely, suppose that we are given a graph G and a source s. We define the level of a vertex v as the shortest distance from s to v, that is the number of edges on the shortest path connecting s to v.

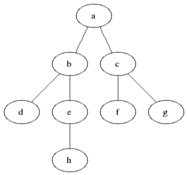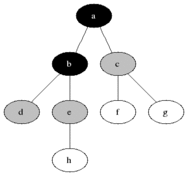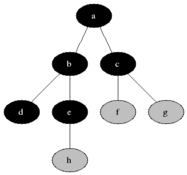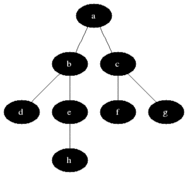
The above animated image provides an insight into the processing steps

• Starting node a is pushed to the queue with level set to 0
• Pop the (node,level) from the queue; at first this is (a,0)
  • Mark node as visited (black)
  • For each edge coming off the node
    • If edge is not visited
      • calculate edge-level as one edge away from node, that is, level + 1
      • push (edge, edge-level) at the end of the queue for processing (gray)

As a result and as depicted below, at the end of the graph processing, all nodes have been allocated into depth levels

Implementation

We still need to have the means to maintain the following information while we are searching the graph

• node state, in terms of processed / not processed
• parent node, that is, the node we visited from
• unit in terms of distance / level

The Tracker structure simplifies managing the node processing state of the graph, and we will use as part of our implementation.

Both Tracker and VecDeque structures are part the Graph processing State structure PDState which in turn, implements the BFSearch abstraction

As a result, the following implementation realises the BFS algorithm

    fn path_distance(&self, start:Node, goal:Node) -> Option<(Vec<Node>, Cost)> {
        /// Structure for maintaining processing state while processing the graph
        struct PDState {
            tracker: Tracker,
            queue: VecDeque<Node>
        }
        /// State Constructor from a given Graph and related the initiation requirements for the algo
        impl PDState {
            fn new(g: &Graph) -> PDState {
                PDState {
                    tracker: g.get_tracker(Undiscovered, 0, None),
                    queue: VecDeque::<Node>::new()
                }
            }
        }
        /// Implementation of Path Search abstraction
        impl BFSearch for PDState {
            type Output = (Vec<Node>, Cost);
            type QueueItem = Node;

            /// Initiate search by pushing starting node and mark it as Discovered
            fn initiate(&mut self, node:Node) -> &mut Self {
                self.queue.push_back(node);
                self.tracker[node].visited(Discovered);
                self
            }

            /// Get the first item from the start of the queue
            fn pop(&mut self) -> Option<Self::QueueItem> { self.queue.pop_front() }

            /// extract Node from the queued Item
            fn node_from_queued(&self, node: &Self::QueueItem) -> Node { *node }

            /// Has it seen before ?
            fn is_discovered(&self, node: NodeType) -> bool { self.tracker[node.into()].is_discovered() }

            /// Process Edge before pushing it at the end of the queue
            fn pre_process_edge(&mut self, src: Node, dst: NodeType) -> bool {
                let level = self.tracker[src].dist + 1;
                // mark visited, calculate distance & store parent for distance
                self.tracker[dst.into()].visited(Discovered)
                    .distance(level)
                    .parent(src);
                true
            }

            /// Construct queued item from Node
            fn node_to_queued(&self, node: Node) -> Self::QueueItem { node }

            /// Push item at the end of the queue
            fn push(&mut self, item: Self::QueueItem) { self.queue.push_back(item) }

            /// Extract path discovered so far
            fn extract_path(&self, start: Node) -> Self::Output { self.tracker.extract(start) }
        }

        // Construct the state structure and search for a path that exists between start -> goal
        PDState::new(self).path_search(self, start, goal )
    }

References: